6  分布のグラフ

ここまで、変数の特徴を数値で表す要約について見てきました。しかし、そのような要約ではデータの特徴を正確に把握することは難しいことが分かりました。

本章以降では、数値ではなくグラフによってデータの特徴を把握する可視化 (visualization) について学びます。

6.1 使用するパッケージ

6.1.1 ggplot2

Rでグラフを作る場合、デフォルトの関数を使うこともできますが、ggplot2と呼ばれるパッケージを使うことも多いです。この資料ではggplot2を使う方法を紹介します。なお、ggplot2はtigyverseに含まれています。

R
library(tidyverse)

6.1.2 matplotlib/seaborn

Pythonの場合、matplotlibというパッケージを使って作図することがデファクト・スタンダードとなっています。また、しばしば、seabornというパッケージを併用して、より柔軟な作図を行うことがあります。

Python
from matplotlib import pyplot as plt

これまでと、やや書き方が異なっています。まず、fromについて説明します。Pythonのパッケージは入れ子構造になっています。つまり、matplotlibというパッケージの中にpyplotというパッケージが含まれています。すなわち、matplotlibの中のpyplotだけを呼び出すという意味です。なお、以下のコードは同じ意味です。

Python
import matplotlib.pyplot as plt

次にasについて説明します。as以下がない場合、pyplotの中の関数などを使う際にはpyplot.と書く必要がありますが、それは面倒な気もします。asで仮名を与えることで、plt.と短縮して書くことができます。別にpltである必要はないのですが、デファクト・スタンダードとして使われています。

Python
import seaborn as sns

6.1.3 お手本を探す

自分でこのようなグラフを作りたいと頭の中にあったとしても、それを作るためのコードを探すのは一苦労です。まずは、「お手本」を見つけて、そのコードを参考にするのがよいでしょう。例えば、以下のようなサイトは「お手本」を探す際に有用です。

その上で分からないことがあれば、公式サイトのreferenceを参照したり、ググります。

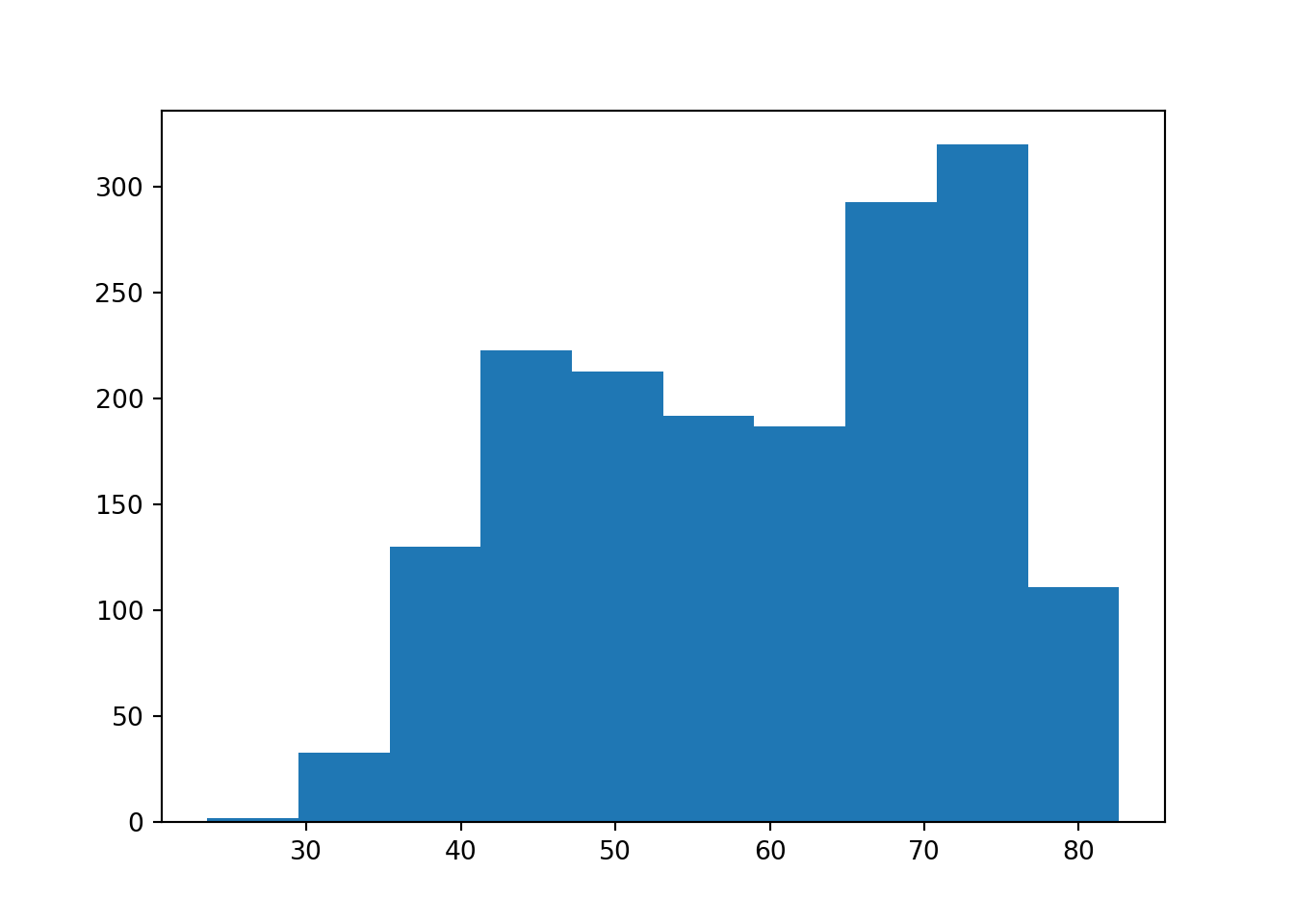
6.2 ヒストグラム

ある1つの変数がどのように散らばっているかを分布 (distribution) と言いますが、これを可視化するものとしてヒストグラム (histogram) があります。

まず、Rでggplot2を使ってヒストグラムを作ります。

R (ggplot2)
ggplot(df_gap) + 
    geom_histogram(aes(x = lifeExp))

  1. まず、ggplot()の中に、作図に使用するデータフレームを入れます。そして、+をつけます。イメージとしてはggplot()でキャンバスを作り、そこに絵を+で重ねていきます。
  2. geom_histogram()でヒストグラムを作図します（geomはgeometoryの略です）。その中でaes()によってどの変数を作図に使うかを示します（aesはaestheticsの略です）。今回はヒストグラムの横軸（x軸）に平均寿命を使うことを支持しています。

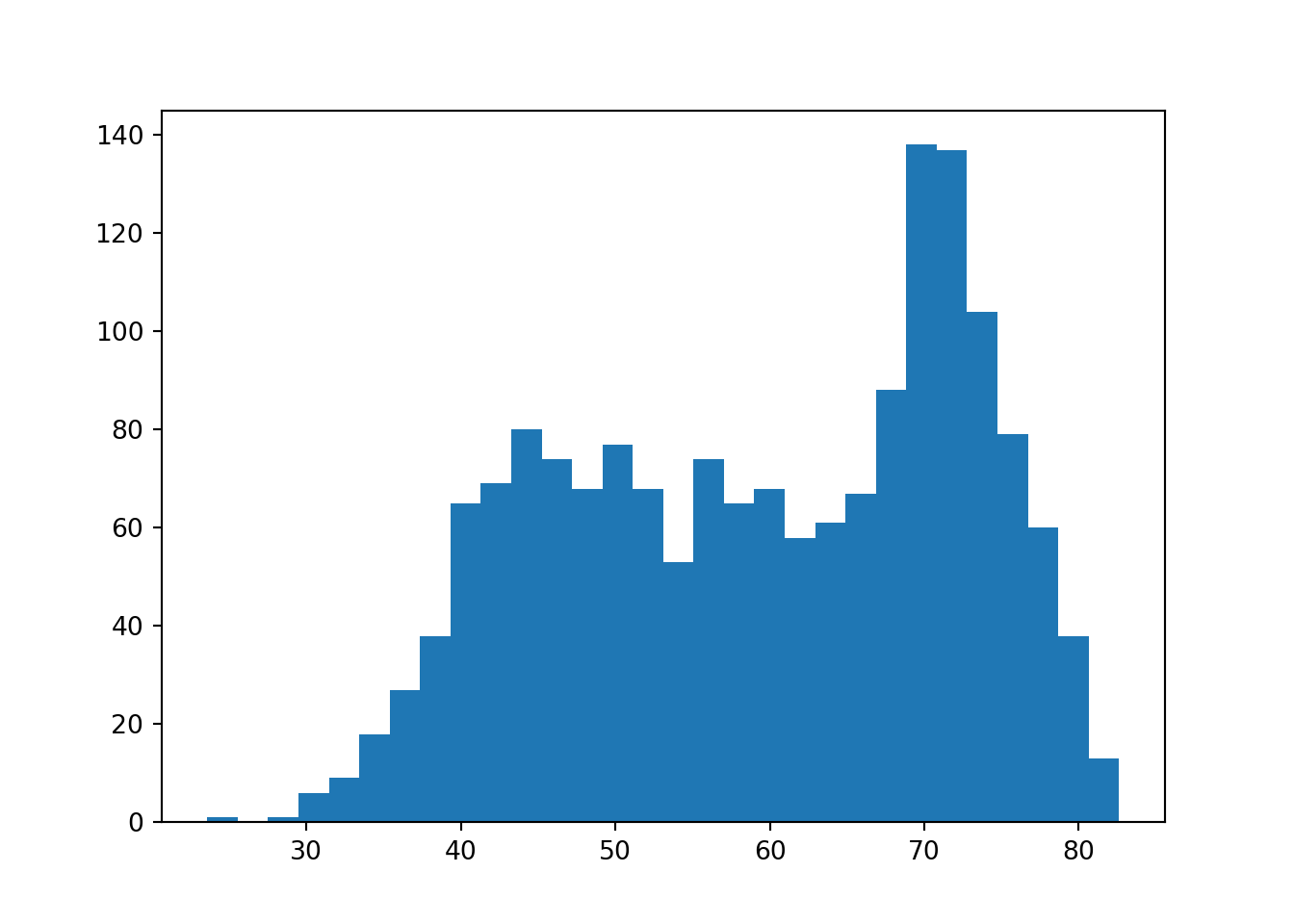
次に、Pythonでmatplotlibを使ってヒストグラムを作ります。

Python (matplotlib)
plt.hist(x=df_gap["lifeExp"])

  • plt.hist()でヒストグラムを作図することを宣言し、その中に平均寿命の変数を入れます。

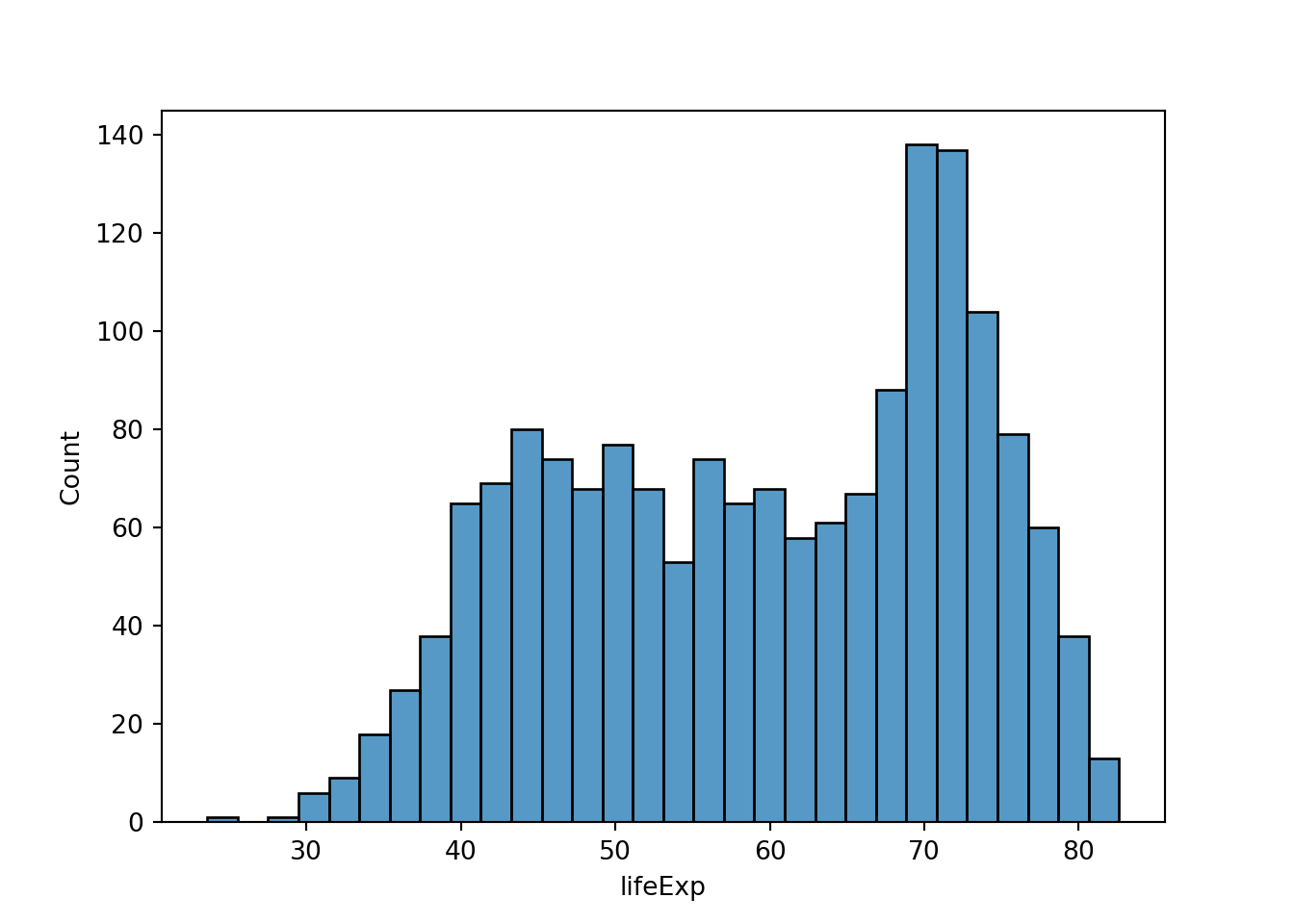
seabornの場合はhistplot()を使って書きます。少しggplot2に近い書き方です。

Python (seaborn)
sns.histplot(df_gap, x="lifeExp")

6.2.1 pandasのメソッド

なお、pandasのデータフレームには作図属性plot()があります。その中のメソッドでヒストグラムを作成できます。

Python (pandas)
df_gap.plot.hist(column="lifeExp")

6.2.2 ビンの幅

ところで、この3つのグラフを見ると、少しずつ異なることが分かります。そもそもヒストグラムとはどのようなグラフなのでしょうか。ヒストグラムでは、まず変数を等間隔のグループに分けていきます。そして、各グループ内で観察の数を数えて、それをy軸に取ります。そうすることで、どのような値を取る観察が多いのかを可視化します。

ヒストグラムではグループを決める幅のことをビンと呼びます。例えば、ggplot2で作図した時に出てくるメッセージを見ると、30個のビンを作っていることが分かります。つまり、平均寿命の値を30等分して、ビンを作っています。

それでは、Pythonでもビンを30個にするとどうなるでしょうか。それぞれのパッケージのreferenceなどを読んでみましょう。

Python (matplotlib)
plt.hist(x=df_gap["lifeExp"], bins=30)

Python (seaborn)
sns.histplot(df_gap, x="lifeExp", bins=30)

仕様のため、厳密には異なりますが、近いグラフが出力されました。

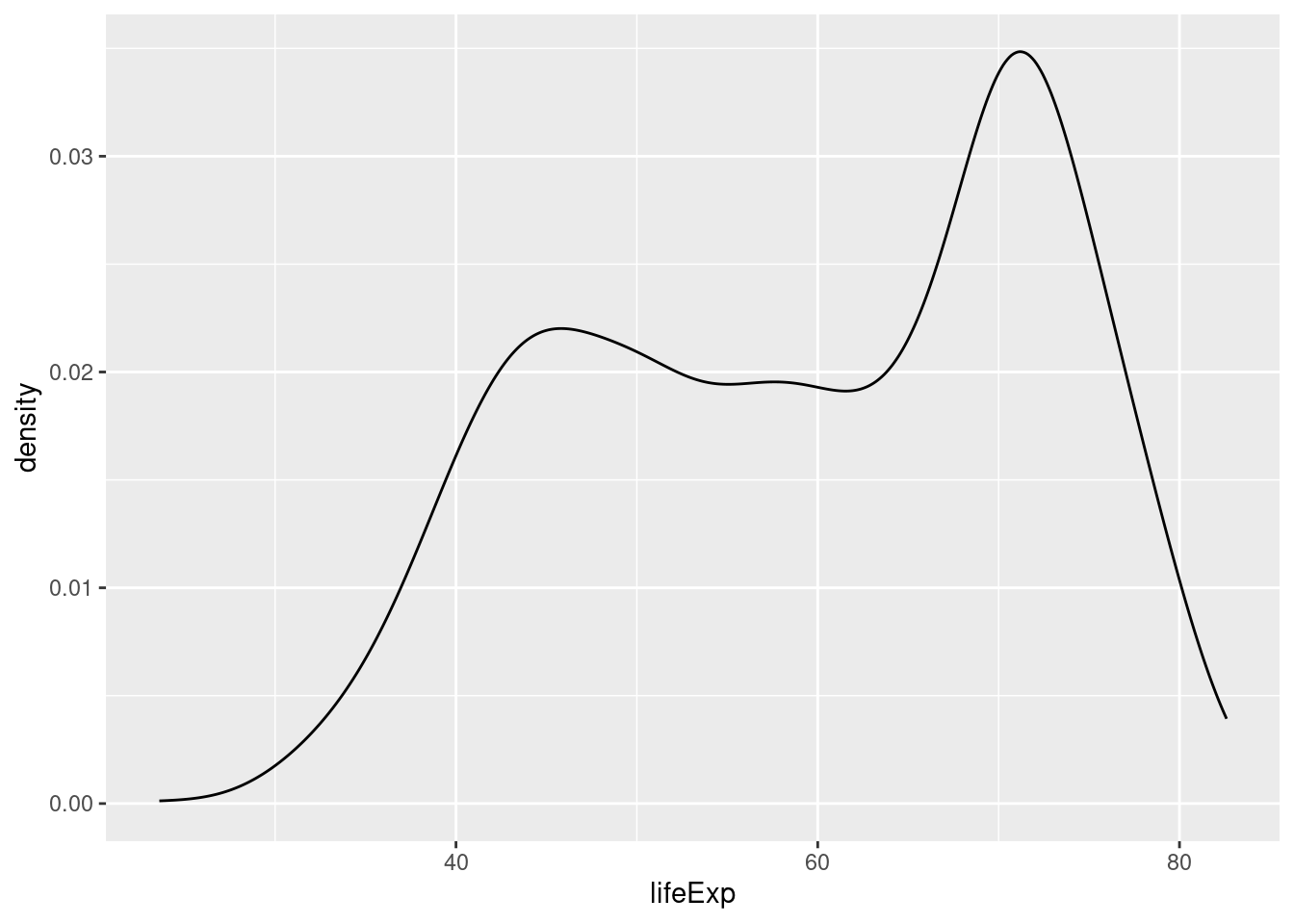
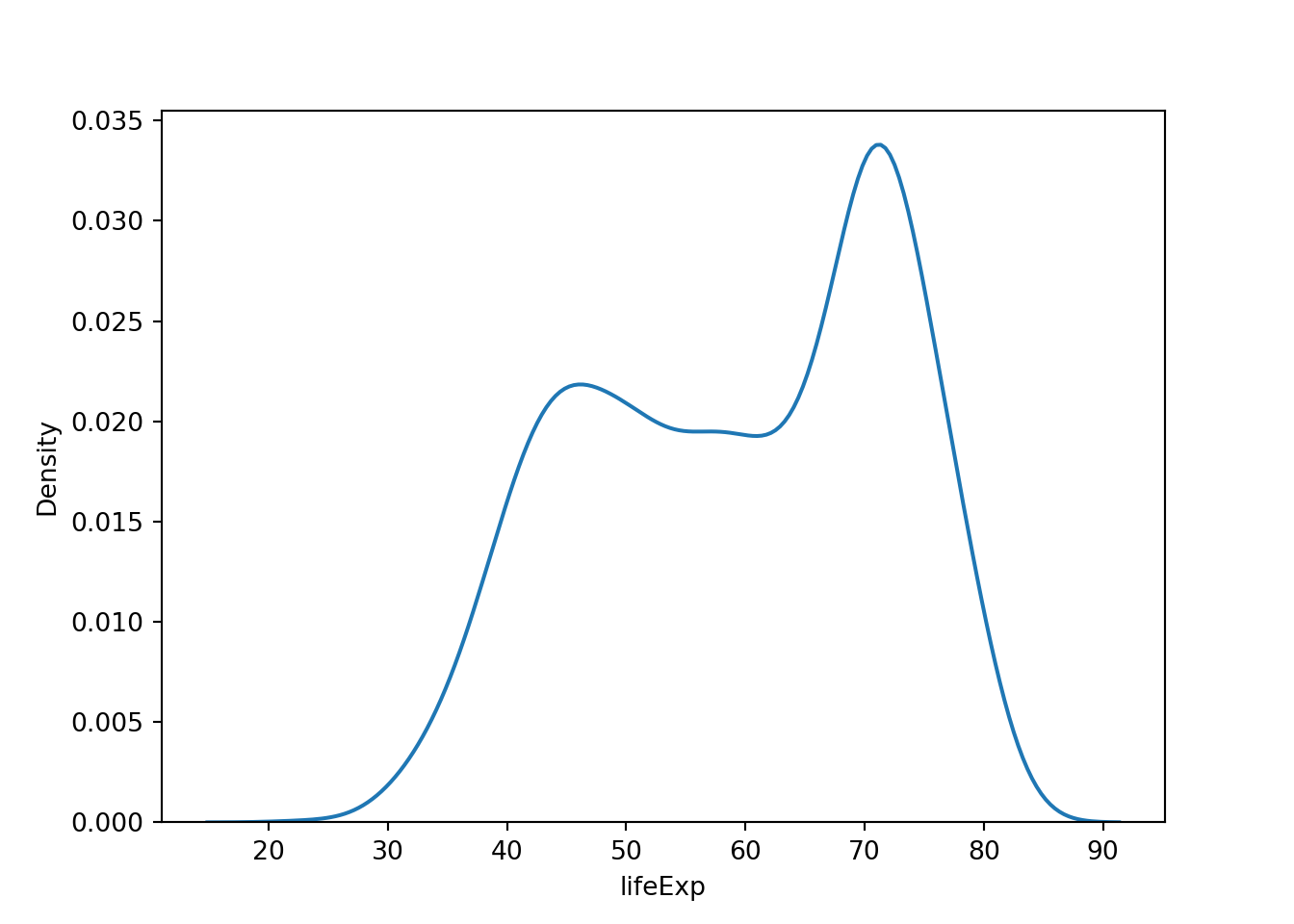
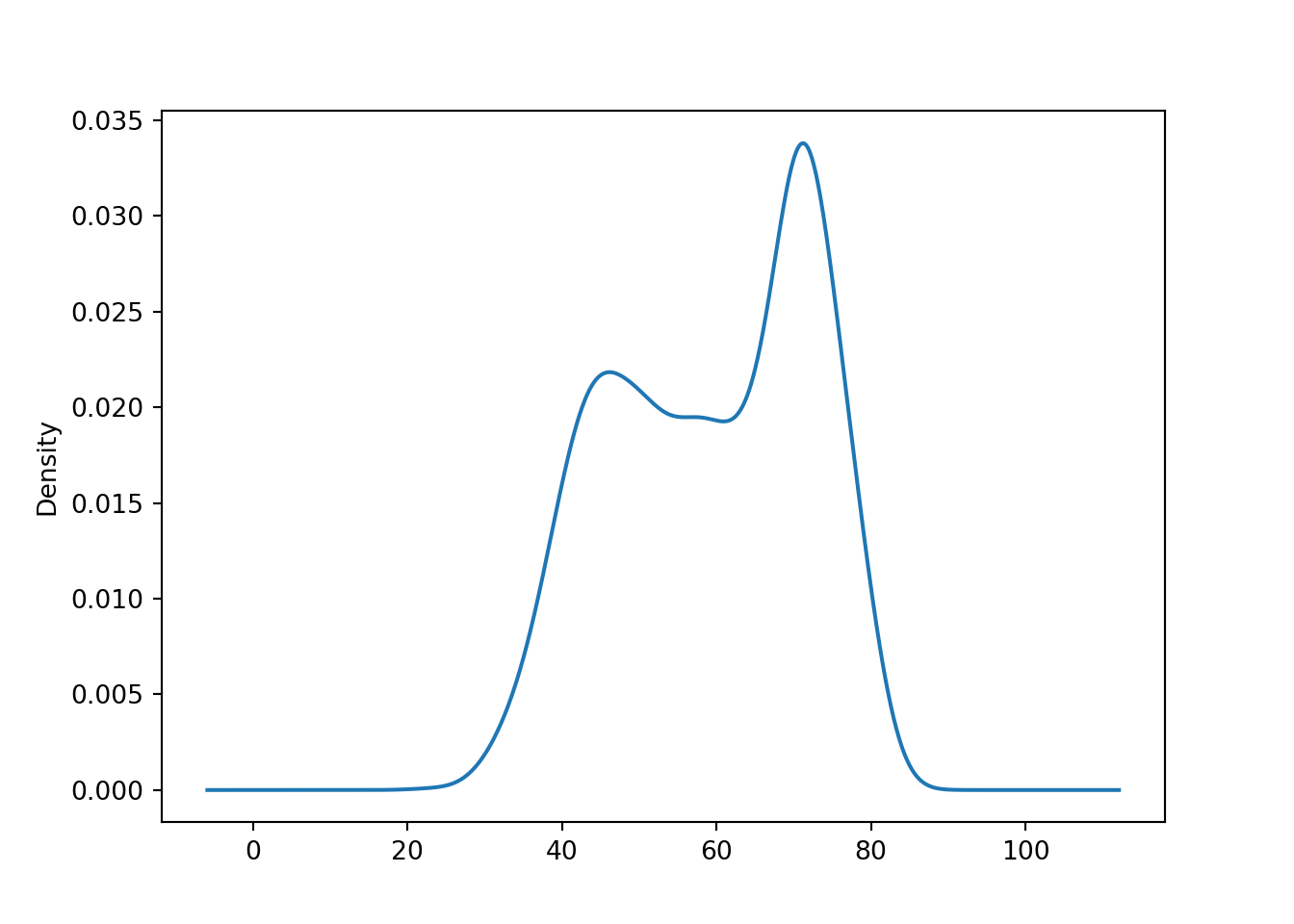
6.3 カーネル密度プロット

ヒストグラムと同じ目的のグラフとしてカーネル密度 (kernel density) プロットというものがあります。直観的に言って、ヒストグラムを「なめらかに」したものです。

R (ggplot2)
ggplot(df_gap) + 
    geom_density(aes(x = lifeExp))

Python (seaborn)
sns.kdeplot(df_gap, x="lifeExp")

mtplotlibでは簡単にカーネル密度を作図することはできませんが、pandasのメソッドでは可能です。

  • あらかじめscipyというパッケージをインストールしておきます。
Python (pandas)
df_gap["lifeExp"].plot.kde()

6.4 可視化と要約統計

平均寿命のヒストグラムやカーネル密度プロットを見ていると、要約統計では不十分であることが分かるかと思います。例えば、45歳付近と75歳付近に2つのピークがありますが、平均値や中央値を使っても、このことは分かりません。

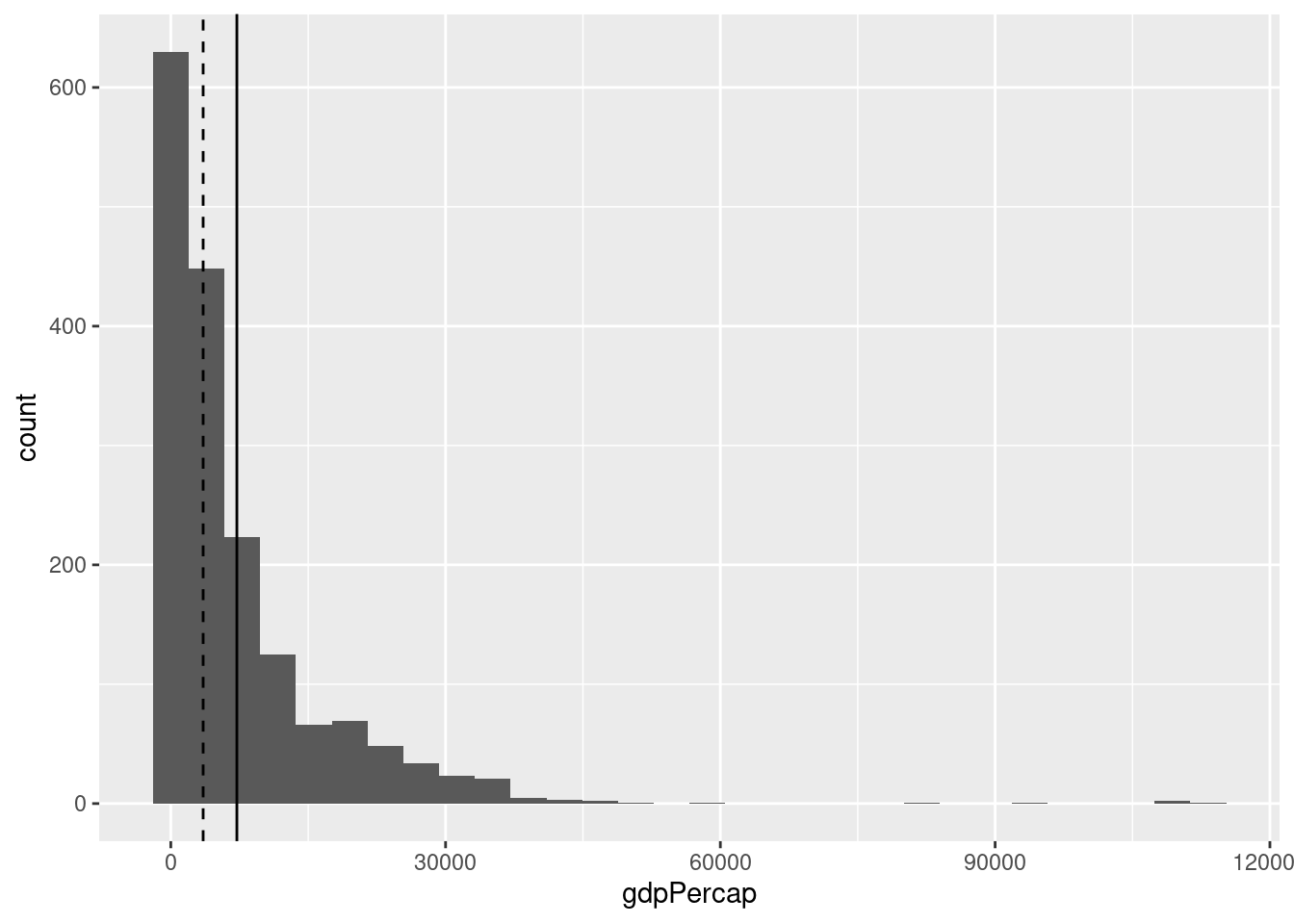
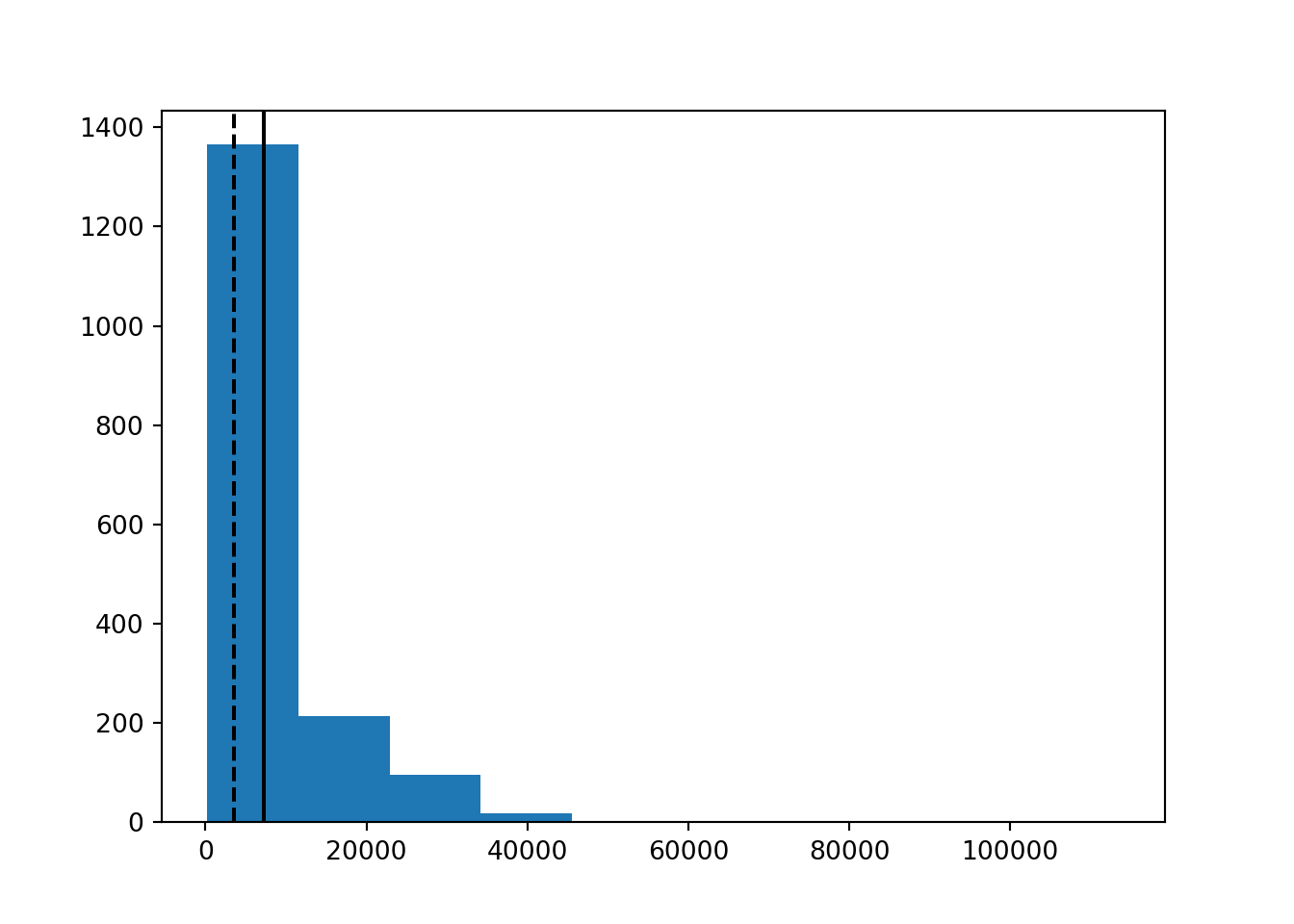
ついでに、平均値と中央値の関係について言及しておきます。以下のグラフは各国の一人あたりGDPの分布のグラフに平均値（実線）と中央値（破線）を縦線で表したものです。

R (ggplot2)
ggplot(df_gap) + 
    geom_histogram(aes(x = gdpPercap)) + 
    geom_vline(aes(xintercept = mean(gdpPercap))) + 
    geom_vline(aes(xintercept = median(gdpPercap)), linetype = "dashed")

  • geom_vline()で垂直な線を作図します。aes()内ではxではなく、xinterceptである点に注意してください。
  • linetypeで線の種類を指定します。
Python (matplotlib)
plt.hist(df_gap["gdpPercap"])
plt.axvline(x = df_gap["gdpPercap"].mean(), color="black")
plt.axvline(x = df_gap["gdpPercap"].median(), color="black", linestyle="dashed")

Python (seaborn)
sns.histplot(df_gap, x="gdpPercap")
plt.axvline(x = df_gap["gdpPercap"].mean(), color="black")
plt.axvline(x = df_gap["gdpPercap"].median(), color="black", linestyle="dashed")

  • matplotlibではplt.axvline()で垂線を描きます（seabornもmatplotlibの一種なので併用できます）。
  • linestyleで線の種類を指定します。

ところで、一人あたりGDPのように極端に大きな（あるいは小さな）値をとる観察がある分布をロングテールと呼んだりします。また、「右（左）裾が長い」とか「右（左）に歪んだ」(right[left]-skewed) 分布と呼ぶこともあります。

このように歪んだ分布の場合、平均値と中央値は一致しません。平均値は大きな（あるいは小さな）値に左右されるので、例えば億万長者がいれば、平均値は大きくなります。一方で、中央値はあくまで50%という位置を表しているので、億万長者がいくら稼いでいても中央値は変わりません。分布が歪んでいる場合（すなわち平均値と中央値が乖離している場合）、どちらに関心があるのかを明確にする必要があるでしょう。

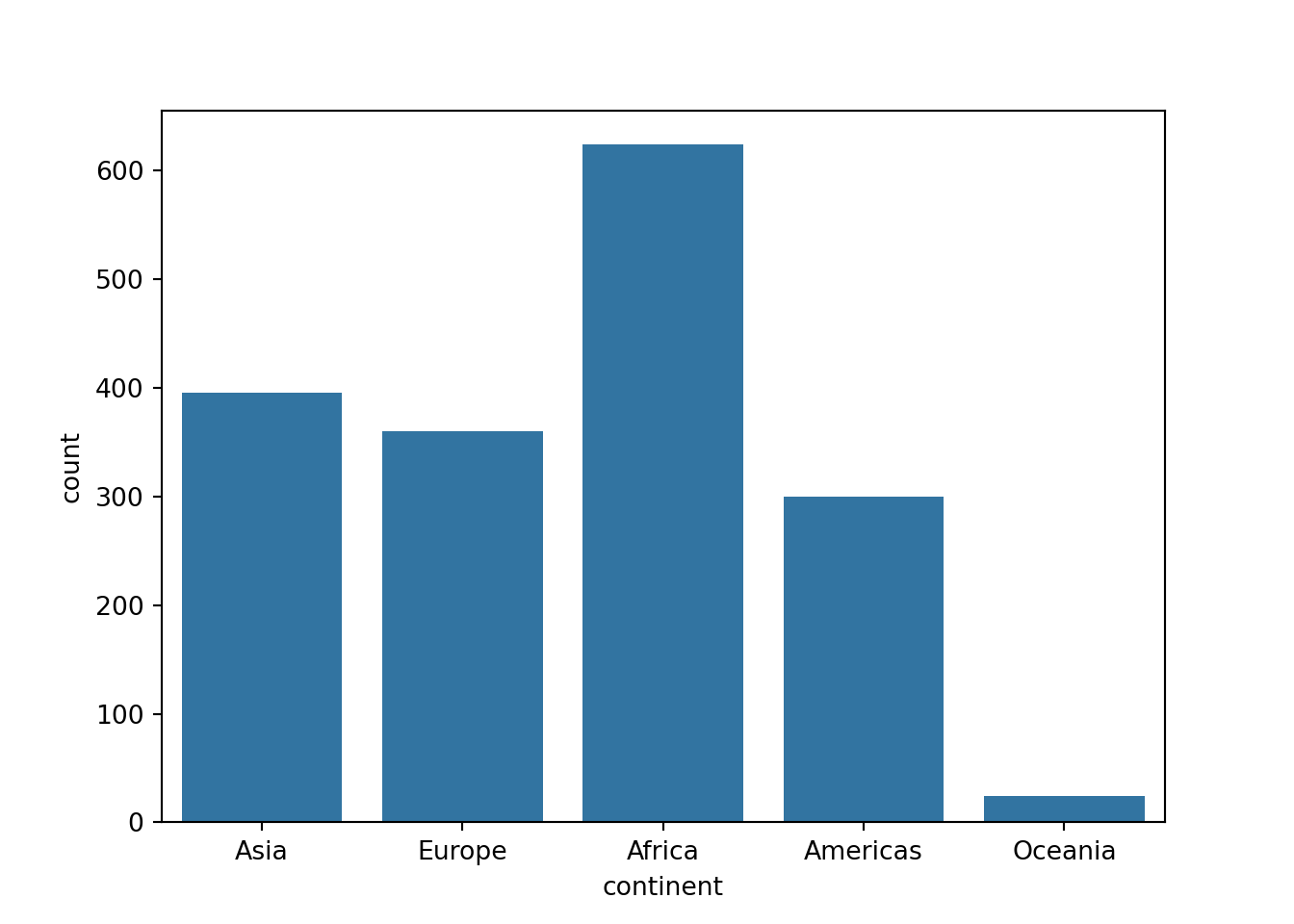
6.5 棒グラフ

ヒストグラムもカーネル密度プロットも連続変数の分布を見るグラフでした。それでは、離散変数の分布も見てみたいと思います（それを分布と呼んでいいのかは分かりませんが）。その場合は棒グラフ (bar chart) を使います。

試しに、大陸ごとの観察数を可視化したいと思います。

R (ggplot2)
ggplot(df_gap) + 
    geom_bar(aes(x = continent))

Python (seaborn)
sns.countplot(df_gap, x="continent")

matplotlibでは、まず集計してから、bar()で作図します。

Python (matplotlib)
df_continent=df_gap.value_counts("continent")

plt.bar(df_continent.index, df_continent.values)

ただ、集計したデータフレームのメソッドで作図もできます。

Python (pandas)
df_continent=df_gap.value_counts("continent")

df_continent.plot.bar()

6.6 グループごとの分布

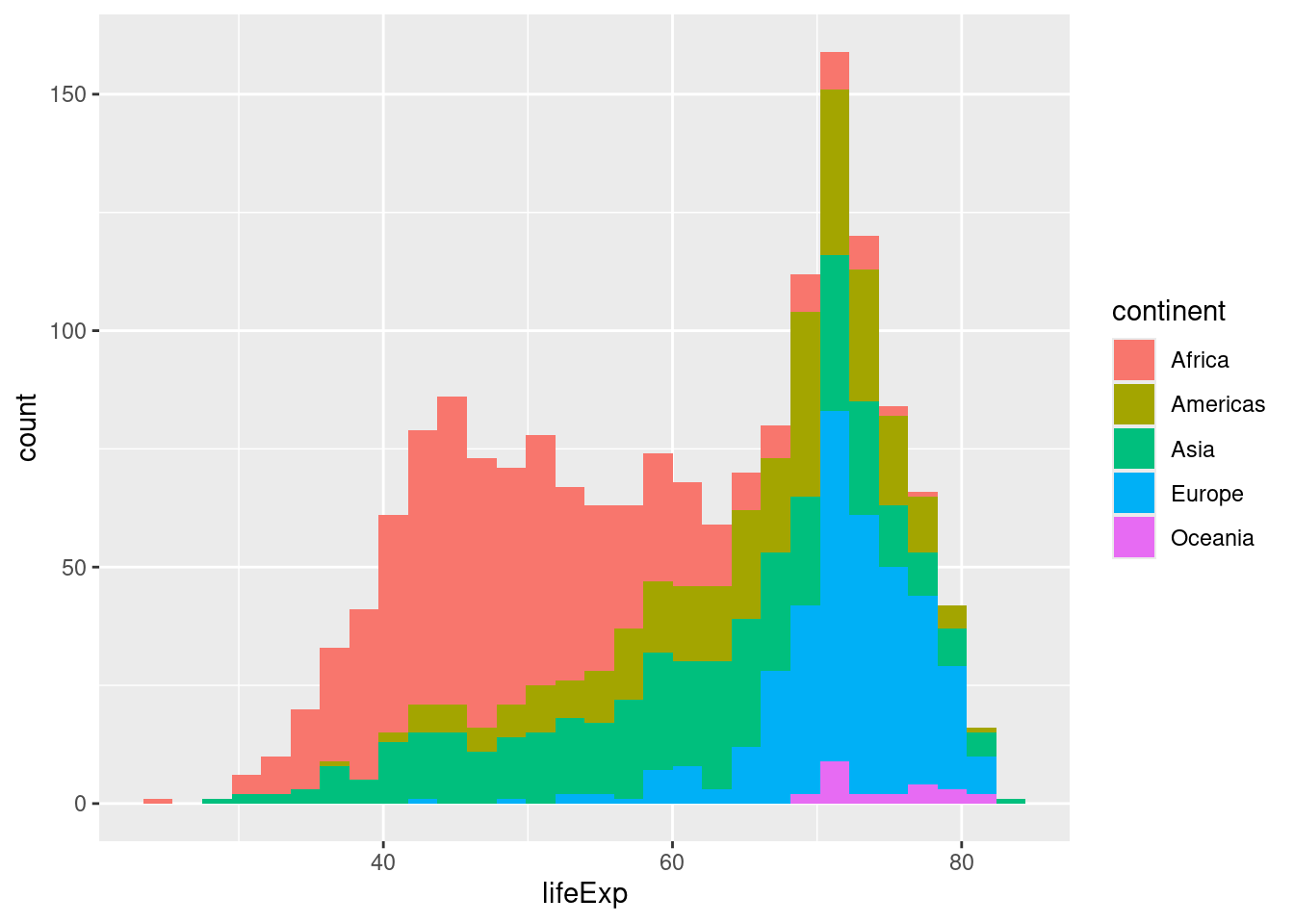
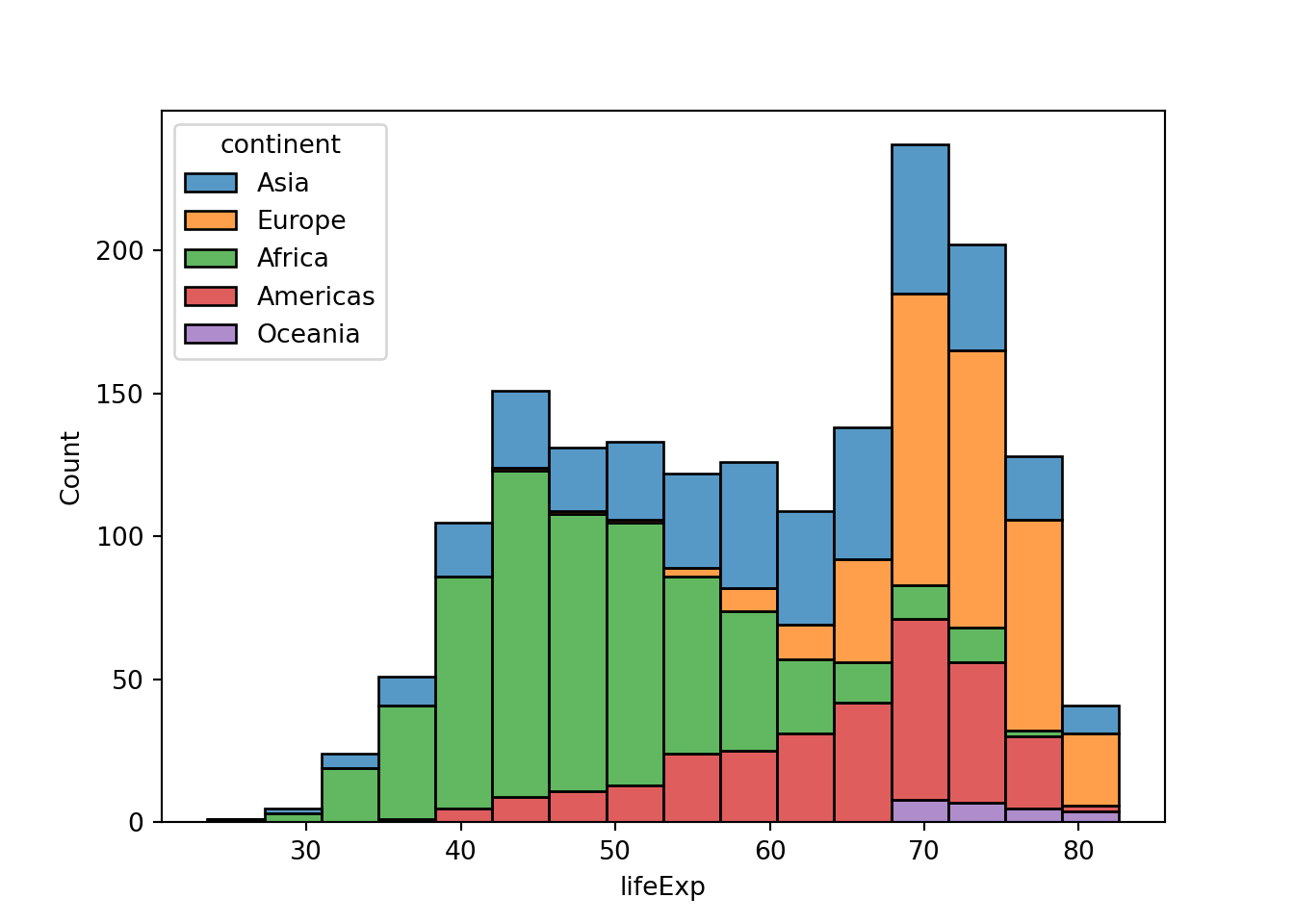
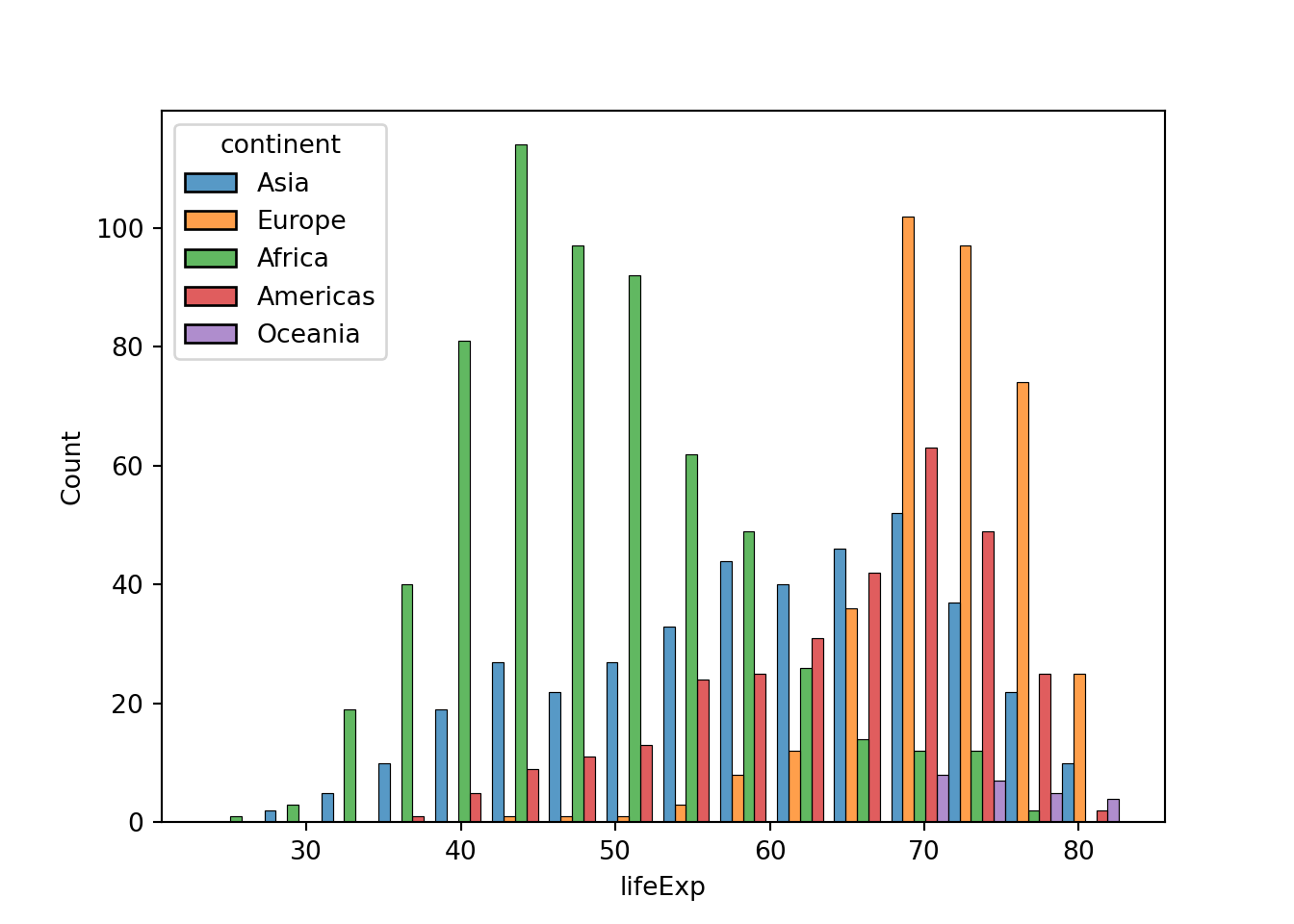
ところで、なぜ平均寿命の分布はフタコブラクダのようになっているのでしょうか。ここでは、地域ごとに異なるという仮説を検討したいと思います。そのために、地域ごとに平均寿命の分布を可視化します。

一つのやり方は地域ごとに色を塗り分けるというものです。もう一つのやり方は地域ごとにグラフを作成するというものですが、これはいずれ扱います。

R (ggplot2)
ggplot(df_gap) + 
    geom_histogram(aes(x = lifeExp, fill = continent))

  • fillで色分けに使う変数を指定します。
Python (seaborn)
sns.histplot(df_gap, x="lifeExp", hue="continent")

  • hueで色分けに使う変数を指定します。

ここから分かることはアフリカの国が左側のコブを作っていて、ヨーロッパやアメリカの国が右側のコブを作っているということでしょう。

ところで、上と下のグラフは少し異なります。上のggplot2のグラフではそれぞれの大陸のデータが積み重なっています。一方で、下のseabornのグラフではそれぞれの大陸のデータが別個に重ねて描かれています。

ggplot2で下のように描くには次のようにします。

R (ggplot2)
ggplot(df_gap) + 
    geom_histogram(aes(x = lifeExp, fill = continent), position = "identity", alpha = 0.5)

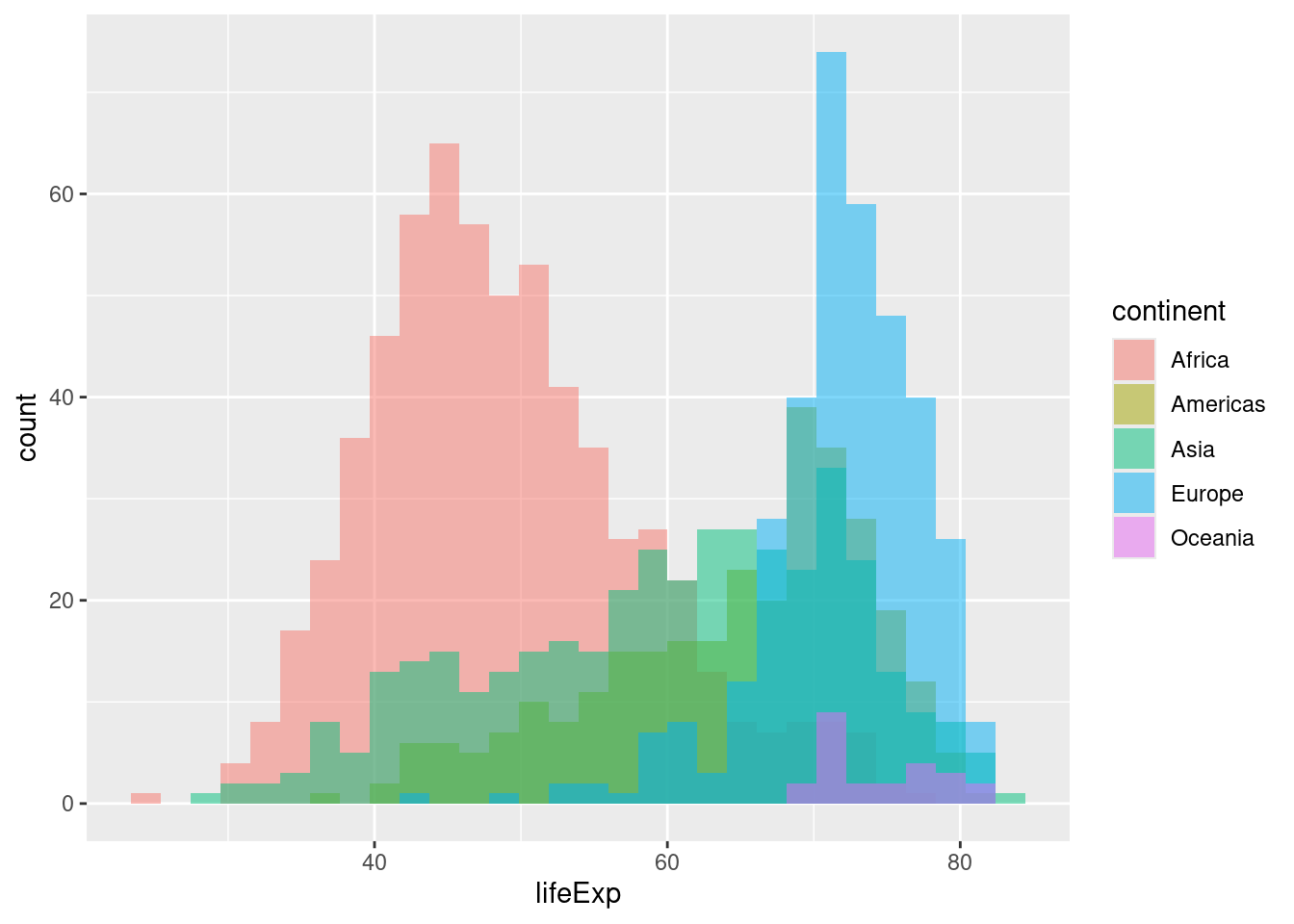
  • position = "identity"によって、そのままの値で作図します。
  • 重ね塗りされるので、alpha = 0.5で少し透過させます。

逆に、seabornで上のように描くには次のようにします。

Python (seaborn)
sns.histplot(df_gap, x="lifeExp", hue="continent", multiple="stack")

  • stacked=Trueあるいはmultiple="stack"で積み重ねて作図します。

あるいは、ggplot2でもseabornでも次のようなグラフを描くこともできます。

R (ggplot2)
ggplot(df_gap) + 
    geom_histogram(aes(x = lifeExp, fill = continent), position = "dodge")

Python (seaborn)
sns.histplot(df_gap, x="lifeExp", hue="continent", multiple="dodge")