5  二変数の要約

多くの場合、変数それ自体ではなく2つ（あるいは複数）の変数の間の関係に関心があることが多いのではないでしょうか。例えば、一人あたりGDPが高いと平均寿命も長くなるのかどうか、など。続いては、このように2つの変数間の関係を要約する方法を学んでいきます。

5.1 連続変数同士の関係

5.1.1 共分散

相関係数 (correlation coefficient) 、特に相関、という言葉は聞いたことがあるでしょう。相関係数とは2つの変数間の関係の強さを見る際に、よく使われる指標です。

これから相関係数について説明しますが、ややこしいので、興味のない人はコードまで飛ばしてください。

まずは、相関係数を理解するために、共分散 (covariance) について学びます。一度、分散の定義に戻ります。

\[ \sigma^2 = \frac{\sum_{i=1}^N (x_i - \bar{x})^2}{N} \]

\(\bar{x}\)は\(x\)の平均でした。したがって、\((x_i - \bar{x})\)は変数の値が平均からどれだけ離れているかを表しており、それを二乗して面積に変換して、その平均を求めることで、変数の散らばり具合を表していました。

共分散は分散の二変数バージョンであり、次のように定義されます。分散との違いは分母の総和の中身が\((x_i - \bar{x})^2\)から\((x_i - \bar{x})(y_i - \bar{y})\)に変わっていることです。

\[ \sigma_{xy}^2 = \frac{\sum_{i=1}^N (x_i - \bar{x})(y_i - \bar{y})}{N} \]

それでは、\((x_i - \bar{x})(y_i - \bar{y})\)について考えたいと思います。この前半は既に述べたように\(x_i\)と平均値との差です。よって、前半は\(x_i\)が平均値よりも大きければ正、小さければ負の値になります。後半については\(x_i\)が\(y_i\)に置き換わっただけで、意味は同様です。

したがって、\((x_i - \bar{x})(y_i - \bar{y})\)全体としては\(x_i\)と\(y_i\)が共に平均値より大きいもしくは小さければ正の値を取ります。一方が平均値より大きく、他方が小さければ負の値を取ります。

より直感的に言えば、\(\bar{x}\)と\(\bar{y}\)を原点とする平面を考えると、\((x_i,y_i)\)が第1（右上）もしくは第3象限（左下）にあるときに、\((x_i - \bar{x})(y_i - \bar{y})\)は正の値を取ります。逆に、第2（左上）もしくは第4象限（右下）にあるときは負の値を取ります。

\((x_i - \bar{x})(y_i - \bar{y})\)の符号

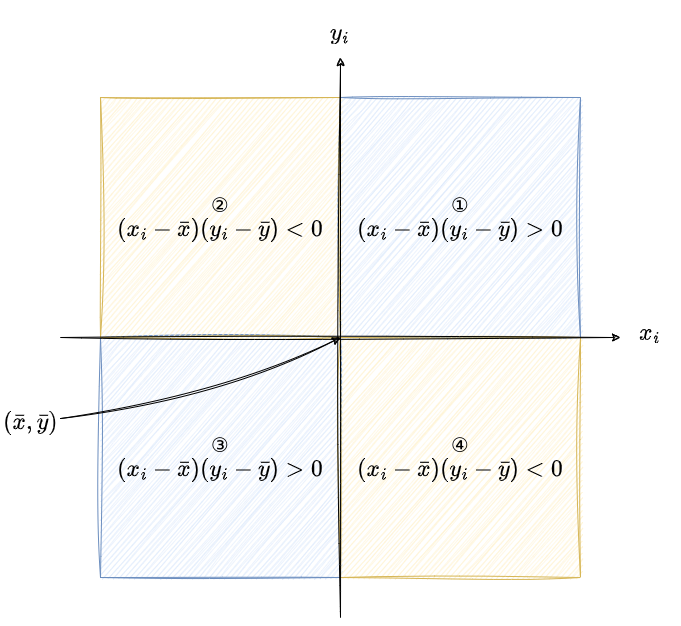
共分散はそのような\((x_i - \bar{x})(y_i - \bar{y})\)の平均値なので、正の値を取るということは\(x\)と\(y\)が正の比例関係にあり、負の値を取るということは負の比例関係にあるということを示唆しています。

5.1.2 複数変数の選択

それでは、共分散を求めたいと思います。平均値や分散を求めるときは1つの変数をデータフレームから取り出しましたが、共分散の場合は2つ（あるいはそれ以上）の変数を取り出す必要があります。RとPythonではそれぞれ、次のように書きます。

R
df_gap[,c("lifeExp", "gdpPercap")]
# A tibble: 1,704 × 2
   lifeExp gdpPercap
     <dbl>     <dbl>
 1    28.8      779.
 2    30.3      821.
 3    32.0      853.
 4    34.0      836.
 5    36.1      740.
 6    38.4      786.
 7    39.9      978.
 8    40.8      852.
 9    41.7      649.
10    41.8      635.
# ℹ 1,694 more rows
  • まず、データフレームの後ろに”[,]`を付けます。
  • ,の左側では横（観察）を選択しますが、今回は全ての観察を用いるので何も指定しません。
  • ,の右側では縦（変数）を選択します。c()の中に変数名オブジェクトを入れることで、複数の変数名のオブジェクトを作成しています。

なお、Rではtidyverseというパッケージ群を使うことで、簡便にデータフレームの処理が可能になります。

tidyverse

tidyverseとは狭義には特定のパッケージの集まりです。広義には既存のRを改善するためのプロジェクトや考え方と言ってもいいかもしれません。

tidyverseは主観的には便利なのですが、Rの標準的な書き方とはやや異なるため、結果的にRを分断しかねない要素もあります。この資料ではtidyverseを使って書こうと思います。

具体的にはtidyverseの中のdplyrというパッケージを使いますが、tidyverseを読み込むだけで関連パッケージが全て読み込まれます。

R
library(tidyverse)

df_gap |> 
    select(lifeExp, gdpPercap)
# A tibble: 1,704 × 2
   lifeExp gdpPercap
     <dbl>     <dbl>
 1    28.8      779.
 2    30.3      821.
 3    32.0      853.
 4    34.0      836.
 5    36.1      740.
 6    38.4      786.
 7    39.9      978.
 8    40.8      852.
 9    41.7      649.
10    41.8      635.
# ℹ 1,694 more rows

pandasでは[.loc[,](https://pandas.pydata.org/docs/reference/api/pandas.DataFrame.loc.html)]メソッドを使います。

Python
df_gap.loc[:,["lifeExp", "gdpPercap"]]
      lifeExp   gdpPercap
0      28.801  779.445314
1      30.332  820.853030
2      31.997  853.100710
3      34.020  836.197138
4      36.088  739.981106
...       ...         ...
1699   62.351  706.157306
1700   60.377  693.420786
1701   46.809  792.449960
1702   39.989  672.038623
1703   43.487  469.709298

[1704 rows x 2 columns]
  • ,の左側では横（観察）を選択しますが、今回は全ての観察を用いるので:を入れます。
  • ,の右側では縦（変数）を選択します。[]の中に変数名オブジェクトを入れることで、複数の変数名のオブジェクトを作成しています。

なお、次のように省略して書くこともできます。

Python
df_gap[["lifeExp", "gdpPercap"]]

5.1.3 共分散（再訪）

共分散を求めます。なお、対角成分（左上や右下など）は分散を示しています。

R
cov(df_gap[,c("lifeExp", "gdpPercap")])
             lifeExp  gdpPercap
lifeExp     166.8517    74323.2
gdpPercap 74323.1957 97169410.1
Python
df_gap.loc[:,["lifeExp", "gdpPercap"]].cov()
                lifeExp     gdpPercap
lifeExp      166.851664  7.432320e+04
gdpPercap  74323.195748  9.716941e+07

ところで、7.432320e+04とはなんぞやと思うかもしれません。これは浮動小数点と呼ばれるもので、\(7.432320...\times10^4 = 74323.20...\)を意味しています。

5.1.4 相関係数

共分散は2つの変数の比例関係を示していますが、一つの問題があります。それは、変数の散らばり具合も含んでいるため、その値の解釈が難しいということです。試しに、人口も含めて共分散を求めてみます。

R
cov(df_gap[,c("lifeExp", "pop", "gdpPercap")])
               lifeExp           pop     gdpPercap
lifeExp   1.668517e+02  8.907024e+07  7.432320e+04
pop       8.907024e+07  1.126950e+16 -2.678859e+10
gdpPercap 7.432320e+04 -2.678859e+10  9.716941e+07

例えば、平均寿命と人口の共分散は\(89070240\)で、平均寿命と一人あたりGDPの共分散は\(74323\)です。では、前者の方が大きな値を取っているので、人口のほうが一人あたりGDPよりも平均寿命と強い関係にあると言っていいでしょうか。もしかすると人口のほうが大きな値を取りやすいので、平均値よりも離れやすく、その結果として共分散も大きくなっているのかもしれません。

そこで、変数の値の大きさに左右されずに関係性を示すものとして相関係数を使いたいと思います。相関係数は共分散を\(x_i\)の分散と\(y_i\)の分散の積で割ったものになります。

\[ \rho_{xy} = {\sigma^2_{xy} \over \sigma_x \sigma_y} \]

直感的に言えば、\(x_i\)の分散と\(y_i\)の分散で割ることによって、\(x_i\)と\(y_i\)の散らばり具合を相殺（調整）しています。結果として、相関係数は\(-1\)から\(1\)の間に収まります。

それでは、相関係数を求めます。人口よりも一人あたりGDPの方が平均寿命と高い相関係数を持っている、すなわち強い関係にあることが分かります。

R
cor(df_gap[,c("lifeExp", "pop", "gdpPercap")])
             lifeExp         pop   gdpPercap
lifeExp   1.00000000  0.06495537  0.58370622
pop       0.06495537  1.00000000 -0.02559958
gdpPercap 0.58370622 -0.02559958  1.00000000
Python
df_gap.loc[:,["lifeExp", "pop", "gdpPercap"]].corr()
            lifeExp       pop  gdpPercap
lifeExp    1.000000  0.064955   0.583706
pop        0.064955  1.000000  -0.025600
gdpPercap  0.583706 -0.025600   1.000000

5.2 可視化の重要性

ところで、これまで「強い関係」という言葉を定義せずに用いていました。重要なことは、相関係数で分かることは「どれくらい2つの変数が直線的な関係にあるか」ということ（だけ）です。

ここで、Wikipediaから画像を拝借して、この点を考えたいと思います。いわゆる散布図 (scatter plot) と呼ばれるもので、横軸が\(x_i\)、縦軸が\(y_i\)を表していると考えてください。

相関係数
  1. まず、1段目を見ると分かるように相関係数は高い（低い）値を取れば取るほど2つの変数は直線に近づいていきます。また、相関係数が正であれば正の比例関係、負であれば負の比例関係にあることも分かります。
    • なお、「どれくらい相関係数が高ければいいのか」というのは意味のない疑問だと思っています。例えば、\(0.8\)でも関係は弱いと思う人もいれば、\(0.4\)でも強いと思う人もいるでしょう。
  2. 続いて、2段目では全ての図において相関係数は\(1\)（もしくは\(-1\)）になっています。ここで異なるのはそれぞれの直線の傾きです。「強い関係」と聞くと傾きが大きいと想像するかもしれませんが、相関係数はそこまで意味しません。
  3. 最後に、3段目では全ての図において相関係数は\(0\)となっています。それぞれ2つの変数は何かしらの関係性を持っていそうですが、相関係数では直線以外の関係性を捉えることはできません。

以上のことをまとめると、相関係数だけで分かることは少ないということではないでしょうか。そして教訓は相関係数という数値だけでなく、実際にグラフを作るということでしょう。

この点をより実感できるものとしてAnscombe”s quartetやDatasaurus Dozenというデータ（およびグラフ）があります。これらのデータは全て同じ平均値や分散、相関係数を持っていますが、それぞれ異なる印象を与えます。

Anscombe”s quartet

Datasaurus Dozen

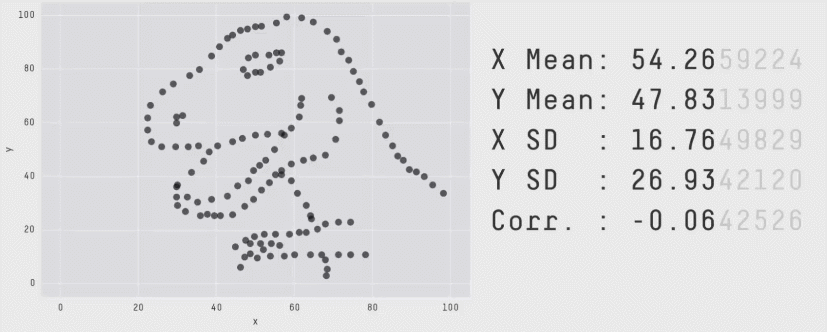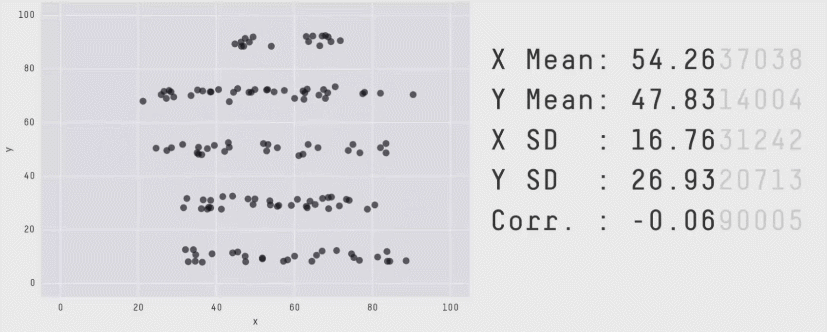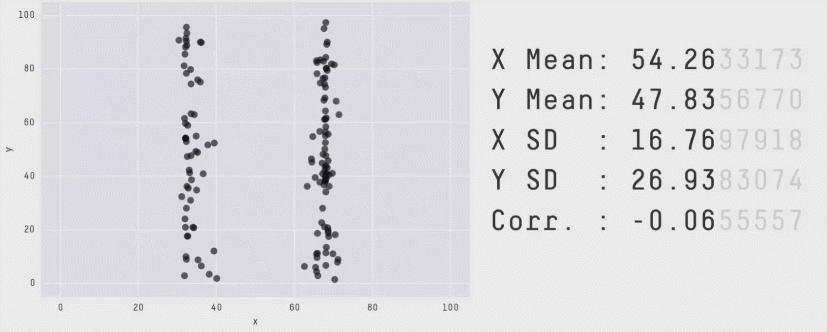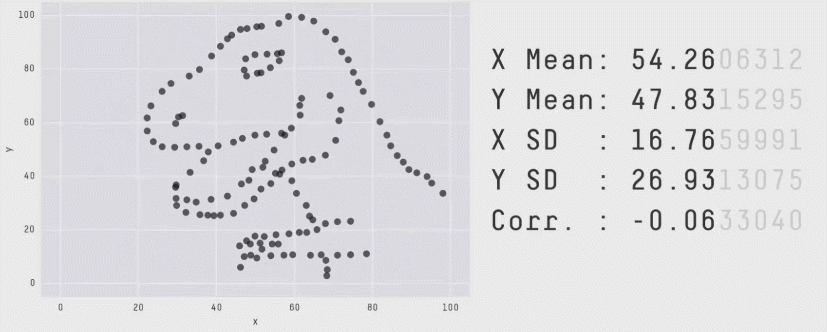
したがって、相関係数だけでなく平均値や分散についても数値だけを見るのではなく、グラフを作って確認するのがよいでしょう。グラフの作成は次章からのテーマです。

5.3 連続変数と離散変数の関係

5.3.1 グループごとの平均値

グループごとに平均値を求めることで、離散変数と連続変数の関係を見ることができます。Rではすでに触れたtidyverseによって簡単に処理できます。

R
df_gap |> 
    group_by(continent) |> 
    summarise(mean_lifeExp = mean(lifeExp), 
              mean_pop = mean(pop), 
              mean_gdpPercap = mean(gdpPercap))
# A tibble: 5 × 4
  continent mean_lifeExp  mean_pop mean_gdpPercap
  <fct>            <dbl>     <dbl>          <dbl>
1 Africa            48.9  9916003.          2194.
2 Americas          64.7 24504795.          7136.
3 Asia              60.1 77038722.          7902.
4 Europe            71.9 17169765.         14469.
5 Oceania           74.3  8874672.         18622.
  • まず、group_by()でどの変数がグループを表しているかを指定します。
  • 次に、summarise()の中で平均値を計算し、新しい変数として定義します。
    • ここでは<-やないんかいと突っ込みたくなりますが、=なので気をつけてください。

pandasではこのように書きます。

Python
df_gap.groupby("continent")[["lifeExp", "pop", "gdpPercap"]].mean()
             lifeExp           pop     gdpPercap
continent                                       
Africa     48.865330  9.916003e+06   2193.754578
Americas   64.658737  2.450479e+07   7136.110356
Asia       60.064903  7.703872e+07   7902.150428
Europe     71.903686  1.716976e+07  14469.475533
Oceania    74.326208  8.874672e+06  18621.609223
  • まず、groupby()でどの変数がグループを表しているかを指定します。
  • 次に[[...]]で平均値を計算したい変数を指定します。
  • 最後に、.mean()で平均値を求めます。

pandasでの集計には注意が必要です。グループとして使った変数continentは集計後のデータフレームでは変数ではなくindexになっています。

  • indexとは各観察（行）を表す目印のようなものです。

グループ化に使った変数をindexとせずに、変数のままにする場合は、次のようにas_index=Falseを付けます。

Python
df_gap.groupby("continent", as_index=False)[["lifeExp", "pop", "gdpPercap"]].mean()
  continent    lifeExp           pop     gdpPercap
0    Africa  48.865330  9.916003e+06   2193.754578
1  Americas  64.658737  2.450479e+07   7136.110356
2      Asia  60.064903  7.703872e+07   7902.150428
3    Europe  71.903686  1.716976e+07  14469.475533
4   Oceania  74.326208  8.874672e+06  18621.609223

平均値だけでなく、その他の要約統計量も同様に計算できます。

5.3.2 グループのネスト

グループを表す変数は1つに限る必要はありません。例えば、各年の各大陸の平均値を求めることも可能です。

R
library(tidyverse)

df_gap |> 
    group_by(continent, year) |> 
    summarise(mean_lifeExp = mean(lifeExp), 
              mean_pop = mean(pop), 
              mean_gdpPercap = mean(gdpPercap))
# A tibble: 60 × 5
# Groups:   continent [5]
   continent  year mean_lifeExp  mean_pop mean_gdpPercap
   <fct>     <int>        <dbl>     <dbl>          <dbl>
 1 Africa     1952         39.1  4570010.          1253.
 2 Africa     1957         41.3  5093033.          1385.
 3 Africa     1962         43.3  5702247.          1598.
 4 Africa     1967         45.3  6447875.          2050.
 5 Africa     1972         47.5  7305376.          2340.
 6 Africa     1977         49.6  8328097.          2586.
 7 Africa     1982         51.6  9602857.          2482.
 8 Africa     1987         53.3 11054502.          2283.
 9 Africa     1992         53.6 12674645.          2282.
10 Africa     1997         53.6 14304480.          2379.
# ℹ 50 more rows
Python
df_gap.groupby(["continent", "year"])[["lifeExp", "pop", "gdpPercap"]].mean()
                  lifeExp           pop     gdpPercap
continent year                                       
Africa    1952  39.135500  4.570010e+06   1252.572466
          1957  41.266346  5.093033e+06   1385.236062
          1962  43.319442  5.702247e+06   1598.078825
          1967  45.334538  6.447875e+06   2050.363801
          1972  47.450942  7.305376e+06   2339.615674
          1977  49.580423  8.328097e+06   2585.938508
          1982  51.592865  9.602857e+06   2481.592960
          1987  53.344788  1.105450e+07   2282.668991
          1992  53.629577  1.267464e+07   2281.810333
          1997  53.598269  1.430448e+07   2378.759555
          2002  53.325231  1.603315e+07   2599.385159
          2007  54.806038  1.787576e+07   3089.032605
Americas  1952  53.279840  1.380610e+07   4079.062552
          1957  55.960280  1.547816e+07   4616.043733
          1962  58.398760  1.733081e+07   4901.541870
          1967  60.410920  1.922986e+07   5668.253496
          1972  62.394920  2.117537e+07   6491.334139
          1977  64.391560  2.312271e+07   7352.007126
          1982  66.228840  2.521164e+07   7506.737088
          1987  68.090720  2.731016e+07   7793.400261
          1992  69.568360  2.957096e+07   8044.934406
          1997  71.150480  3.187602e+07   8889.300863
          2002  72.422040  3.399091e+07   9287.677107
          2007  73.608120  3.595485e+07  11003.031625
Asia      1952  46.314394  4.228356e+07   5195.484004
          1957  49.318544  4.735699e+07   5787.732940
          1962  51.563223  5.140476e+07   5729.369625
          1967  54.663640  5.774736e+07   5971.173374
          1972  57.319269  6.518098e+07   8187.468699
          1977  59.610556  7.225799e+07   7791.314020
          1982  62.617939  7.909502e+07   7434.135157
          1987  64.851182  8.700669e+07   7608.226508
          1992  66.537212  9.494825e+07   8639.690248
          1997  68.020515  1.025238e+08   9834.093295
          2002  69.233879  1.091455e+08  10174.090397
          2007  70.728485  1.155138e+08  12473.026870
Europe    1952  64.408500  1.393736e+07   5661.057435
          1957  66.703067  1.459635e+07   6963.012816
          1962  68.539233  1.534517e+07   8365.486814
          1967  69.737600  1.603930e+07  10143.823757
          1972  70.775033  1.668784e+07  12479.575246
          1977  71.937767  1.723882e+07  14283.979110
          1982  72.806400  1.770890e+07  15617.896551
          1987  73.642167  1.810314e+07  17214.310727
          1992  74.440100  1.860476e+07  17061.568084
          1997  75.505167  1.896480e+07  19076.781802
          2002  76.700600  1.927413e+07  21711.732422
          2007  77.648600  1.953662e+07  25054.481636
Oceania   1952  69.255000  5.343003e+06  10298.085650
          1957  70.295000  5.970988e+06  11598.522455
          1962  71.085000  6.641759e+06  12696.452430
          1967  71.310000  7.300207e+06  14495.021790
          1972  71.910000  8.053050e+06  16417.333380
          1977  72.855000  8.619500e+06  17283.957605
          1982  74.290000  9.197425e+06  18554.709840
          1987  75.320000  9.787208e+06  20448.040160
          1992  76.945000  1.045983e+07  20894.045885
          1997  78.190000  1.112072e+07  24024.175170
          2002  79.740000  1.172741e+07  26938.778040
          2007  80.719500  1.227497e+07  29810.188275

しかし、ここまで多いとよく分からないので、やはりグラフにするのが人類には優しいのでしょう。

5.4 平均値や分散、共分散の性質 (optional)